미분
미분계수의 기하학적 의미
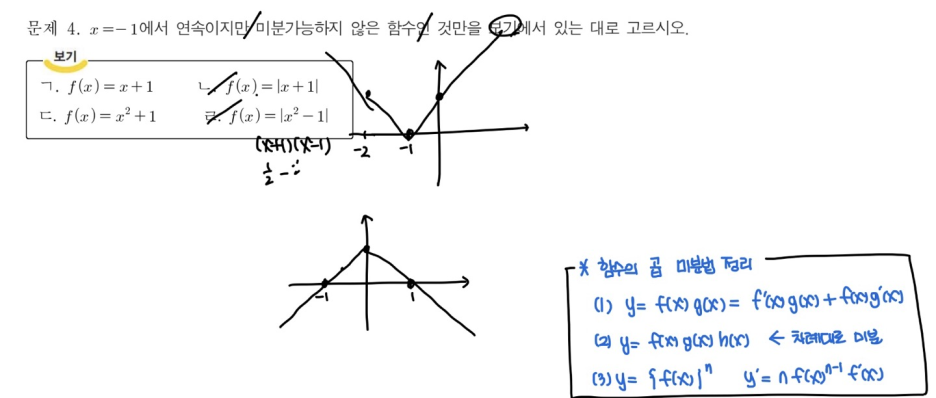
미분가능하면 연속이다. 그러나 연속이지만 미분가능하지 않은 함수도 있다.
[기본 식1]
$ ($$ \lim_{n \to \infty} (1+\dfrac{1}{x})^x $$ = e $
$ ($$ \lim_{t \to \infty} (1+t)^\dfrac{1}{t} $$) = e $
$ ($$ \lim_{t \to \infty} (1+\dfrac{a}{x})^\dfrac{x}{a} $$) = e $
$ ($$ \lim_{t \to \infty} (1+\dfrac{1}{ax})^ax $$) = e $
$ ($$ \lim_{t \to \infty} (1+ax)^ \dfrac{1}{ax} $$) = e $

[기본식 2]
$ ($$ \lim_{n \to 0} \dfrac{ln (1+x)} {x} = 1 $
$ ($$ \lim_{n \to 0} x \; \dfrac {log_{a}{ (1+x) }} {x} = \dfrac{1}{ln \; a} $
$ ($$ \lim_{n \to 0} x \; \dfrac {log_{a}{ (1+kx) }} {x} = k $
$ ($$ \lim_{n \to \infty} x \; ln{ (1+ \dfrac{1}{x} ) } = 1 $
[수업 외 참고식]
$ ($$ \lim_{n \to \infty} \dfrac{e^x \; - \; 1} {x} = 1 $
$ ($$ \lim_{n \to \infty} \dfrac{e^{kx} \; - \; 1} {x} = k $
$ ($$ \lim_{n \to \infty} \dfrac{a^x \; - \; 1} {x} = ln \; a $
로그함수, 지수함수의 미분
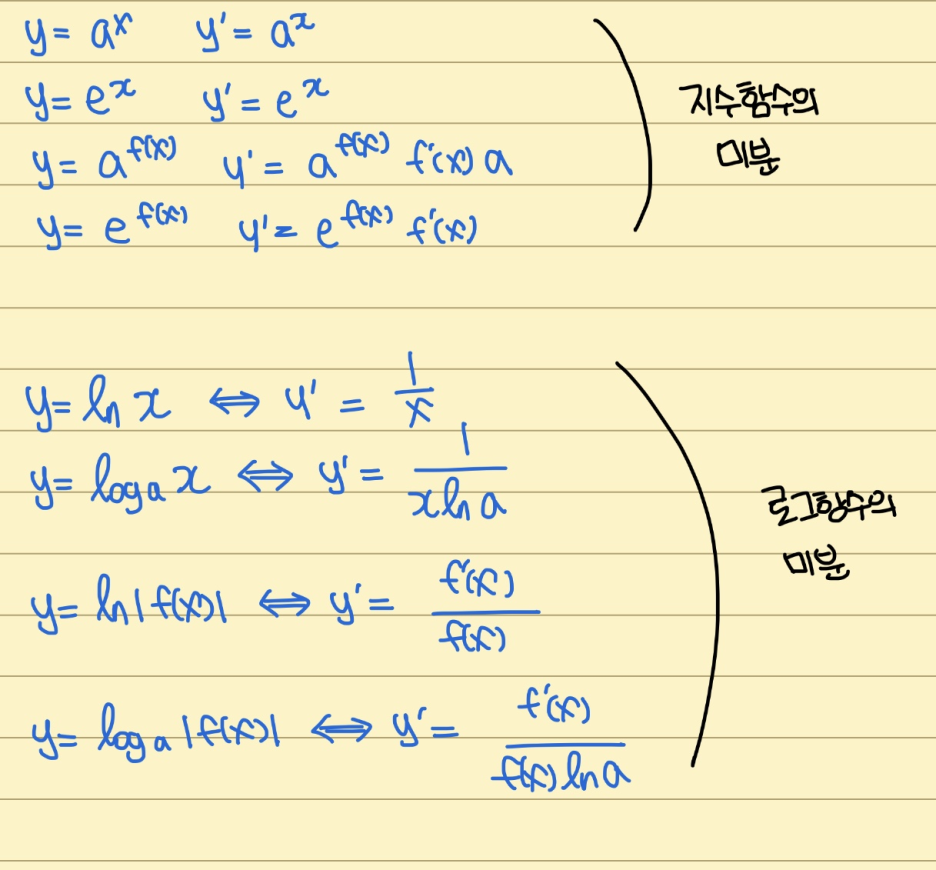

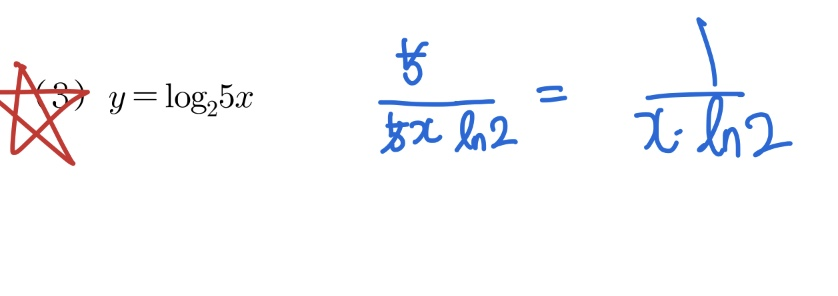
미분의 의미
함수 y= f(x) 일때 y에 대해서 미분한다고 하면, y' = $ \dfrac{dy}{dx} $


참고개념


'개념 정리 > 선수수학' 카테고리의 다른 글
| 2022.05.03 순열파트 암기사항 (0) | 2022.05.09 |
|---|