*앙상블: 주어진 자료로부터 여러 개의 예측모형들을 만든 후 예측모형들을 조합하여 하나의 최종 예측모형을 만드는 방법으로 다중 모델 조합(combining multiple models),분류기 조합(classifier combination)이 있다.
1.정의
배깅은 붓스트랩(Bootstrap) 샘플링을 이용하여 주어진 하나의 데이터로 학습된 예측모형보다 더 좋은 모형을 만들 수 있는 앙상블 기법이다.
a.배깅(Bagging)은 붓스트랩(Bootstrap) 샘플링을 이용한 앙상블 기법이다.
학습데이터 L ={( x_{i},y_{i} ) |i =1,...,n}가 있다고 하자. 이때 학습데이터 L에 대하여 붓스트랩(Bootstrap) 샘플링을 수행하여 B개의 붓스트랩 샘플 데이터 셋( $L_{1},L_{2},...,L_{B}$) 을 만들게 된다. $L_{B}$(b=1,...,B)가 갖고 있는 데이터 개수 n이며 L과 같다. 배깅은 각 셋에 대하여 학습한 모형
배깅에서 집계 방식은 회귀 문제인 경우
$ϕB(x) = \frac{1}{B}\sum_{b=1}^{B}ϕ(x,L_{b})$
분류인 경우
$ϕB(x) = Modeϕ(x,L_{b})$
이다. 여기서 Mode는 최빈값을 나타낸다.
아래 그림은 배깅의 과정을 나타낸다.

b.배깅으로 만든 예측 모형이 주어진 데이터 하나로 학습할 때 보다 더 좋은 성능을 낼 수 있다.
배깅은 일반적으로 하나의 학습 데이터를 가지고 만든 예측모형모다 더 좋은 성능을 낼 수 있다. 특히 회귀문제에서는 평균 제곱 오차(Mean Squared Error)를 계산하여 이를 확인해 볼 수 있다.
학습 데이터 L안에 개별 샘플(x,y)가 확률분포 P로부터 독립적으로 생성되었다고 하자. 여기서 y는 연속형 실수이다. 이때 L을 이용한 예측모형을
이제 (x,y)를 고정시키고 평균 제곱 오차(Mean Squared Error)를 계산하면 다음과 같다.
$$E_{L}(y-ϕ(x,L))^2 \geq (y-ϕ_{A}(x))^2$$ (1)
위쪽 양번 기대값 $E_{p}$을 취하면 $ϕ_{A}$의 평균 제곱 오차가 원래 학습 데이터 하나 가지고 만든 예측모형의 평균 제곱 오차보다 작다는 것을 알 수 있다. $ϕ_{A}$의 추정치는 $ϕ_{B}$라 할 수 있으므로 배깅을 이용한 예측모형의 평균 제곱 오차가 단독 모형의 평균 제곱 오차보다 작다는 것을 추측할 수 있다.
분류 문제인 경우 성능 척도로 0-1손실 함수를 고려하는데 위와 같이 나타날 수 없다. 하지만 Breiman은 좋은 분류기를 가지고 배깅 분류기를 만들면 단독 분류기보다 성능이 더 좋아질 수 있다고 했다.
2.배깅(Bagging)의 특징
a.불안정한 모형일 수록 더 좋은 성능을 발휘한다.
배깅은 불안정한 모형일 수록 더 좋은 모형을 만들어 낼 수 있다. 회귀문제에서는 (2)를 통하여 배깅의 성능이 일반적으로 좋다는 것을 알아 보았다. 이때 성능 향상이 얼마나 되는지는 위에서 증명할 때 상요된 젠센 부등식에서 좌변이 우변보다 얼마나 차이나는지에 달려있다. 이때 (3)번식을 다시 쓰면 (4)번과 같다.


$E_{L}{ϕ_{}}^{2}$(x,L)이 $E(_{L}ϕ (x,L))^{2}$보다 많이 크다는 것은 (4)을 통해 ϕ(x,L)의 변동이 크다는 것을 의미한다. 이는 곧 모형이 불안정하다는 뜻이며 배깅의 성능향상을 도모할 수 있음을 의미한다.
의사결졍나무와 같은 불안정한 모형이 배깅으로 인한 성능 효과가 더 좋을 수 있다.
b.편의(Bias)는 유지하면서 분산(Variance)은 줄인다.
배깅은 (회귀무제에서) 평균 제곱 오차(Mean Squared Error:MSE)가 단독 모형의 MSE보다 작다고 한다. 일반적으로 MSE는 모형의 편향과 분산으로 합으로 나타낼 수 있다. 이때 배깅은 단독 모형들의 평균을 취하므로 직관적으로 편의는 유지한다고 볼 수 있다. 따라서 배깅의 MSE가 줄어든다는 것은 결국 분산을 줄인다고 생각할 수 있다.
즉, 배깅은 편향(Bias)는 유지하면서 분산(Bias)는 줄인다고 생각할 수 있다.
C.별도의 검증 데이터(Validation Set)없이 Out of Bag 데이터를 Hyper Parameter를 최적화하거나 성능 검증을 할 수 있다.
학습 데이터 L의 붓스트랩 샘플 $L_{b}$는 L과 당연히 다를 수 있다. 즉,L이 포함된 데이터가 $L_{b}$에는 포함되지 않을 수 있는 것이다. 이때 L-$L_{b}$ = L $\sqcap $ $L_{b}^{c}$ 를 Out of Bag(OOB)데이터라고 한다. 이때 Out of Bag데이터가 얼마나 많은지 궁금할 수 있다.
문제를 단순화 해보자. L = {1, ..., n} 에서 n개를 복원 추출한 붓스트랩 샘플을 S = s1, ..., $S_{n}$ 라 하자. 이때 Out of Bag데이터의 비율을 알기 위해서는 고정된 m $\in $ {1, ..., n}에 대하여 아래의 확률을 계산해야 한다.

즉, 각 붓스트랩 샘플에 대하여 OOB데이터의 비율은 $e_{}^{-1}$ ~0.632인 것이다. 이는 모의실험을 통해서도 확인할 수 있다. 아래 파이썬 코드는 n의 크기에 따른 OOB데이터의 비율을 계산하여 그래프로 나타낸 것이다.
import numpy as np
import random
import matplotlib.pyplot as plt
from tqdm import tqdm
random.seed(100)
sample_size = np.linspace(1, 1000, 1000, endpoint=True)
ratio_list = []
for n in tqdm(sample_size, total=len(sample_size)):
lst = range(int(n)) ## original data
bs = random.choices(lst, k = len(lst)) ## boostrap sample data
ratio = len(set(lst)-set(bs))/len(lst)
ratio_list.append(ratio)
fig = plt.figure(figsize=(12,6))
fig.set_facecolor('white')
ax = fig.add_subplot()
ax.plot(sample_size, ratio_list, marker='o', markersize=5)
ax.axhline(np.exp(-1), color='red', linestyle='--')
ax.set_xlabel('Sample Size')
plt.show()
위 그래프에서 빨간 점선은 $e_{}^{-1}$ 에 수렴하는 것을 알 수 있다.
이를 통해 알 수 있는 것은 한 붓스트랩 샘플에 대해서 36.8%의 데이터를 버리는 셈이 된다는 것이다. 그렇다면 이 데이터를 이용할 수 없을까? 일종의 성능 지표(테스트 셋이 아닌 검증 데이터 용도로)사용할 수 있다. 어떻게 활용되는지 살펴보자.
OOB의 활용
b=1, ... , B 에 대하여 $O_{b}$ =L - $L_{b}$를 이용하여 학습한 예측모형을 ϕ(x,$L_{b}$)라 하자.이때 (x,y) $\in $ $O_{b}$ 을 이용하여 성능지표 $e_{b}$를 계산한다. 회귀의 경우 평균 잔차 제곱,분류 문제에서는 오분류율이 될 수 있을 것이다.
이제 성능 지표의 평균
$$\bar{e} = \frac{1}{B}\sum_{b=1}^{B}e_{b}$$
을 배깅을 통해 얻어진 모형의 성능 지표로 활용한다.

d.배깅에는 가지치기가 필요 없다.
앞의 a,b를 종합하면 배깅에서 개별 모형은 편의가 작고 분산이 클수록 배깅으로 인한 성능 향상이 커진다는 것을 알 수 있다.기본 학습기(Base Learner)를 의사결정나무(Decision Tree)로 한다고 생각해보자. 의사결정나무 깊이가 깊어질수록 편의는 작아지지만 분산이 커진다. 따라서 이 자체로 배깅에 유리한 개별 모형이기 때문에 이를 추가적으로 가지치기 할 필요가 없어지는 것이다.
3.그 밖에 고려사항
배깅에서 정해야할 것 중 하나가 붓스트랩 샘플들의 개수(Bootstrap Replicates) 일 것이다. OOB를 통하여 를 Hyper Parameter로 놓고 최적화된 를 선택할 수도 있을 것이다. Breiman은 회귀 문제에서는 가 클 필요가 없다고 한다(문맥상 50개 이하인 듯하다).그리고 분류 문제에서는 클래스의 개수가 늘어날 수록 도 크게 하는 것이 좋다고 감각적으로 추측했다. 또한 임계점을 지나고 나서는 를 크게 늘려도 성능 향상이 더 이상 일어나지 않음을 보였다.
4.장단점
장점
a.배깅(Bagging)은 유연하다.
배깅에서 사용할 수 있는 기본 학습기의 종류에는 제한이 없다. 즉, 의사결정나무(Decision Tree)이외에도 분류문제인 경우 로지스틱회귀모형,회귀문제인 경우 선형 회귀 모형이나 Nearest Neighbor방법을 써도 좋다.
b.별도의 검증 데이터 없이 Hyper Parameter를 최적화하거나 성능 평가 가능
OOB 데이터를 이용하면 굳이 학습 데이터를 쪼개지 않더라도 배깅 모형의 성능을 평가나 Hyper Parameter를 최적화할 수 있다.
c. 구현이 어렵지 않다.
배깅 알고리즘이 어렵지 않아서 구현이 쉬운 편에 속한다.
d. 불안정성 모형을 기본 학습기로 사용하는 경우 성능을 크게 향상할 수 있다.
단점
a. 해석이 어렵다.
배깅도 앙상블 기법으로써 앙상블의 고질적인 단점은 바로 해석이 어렵다는 것이다.
b. 성능 향상을 항상 보장하는 것은 아니다.
안정적인 모형(예 : Nearest Neighbor)에 대해서는 성능 향상이 어려울 수 있다

예제


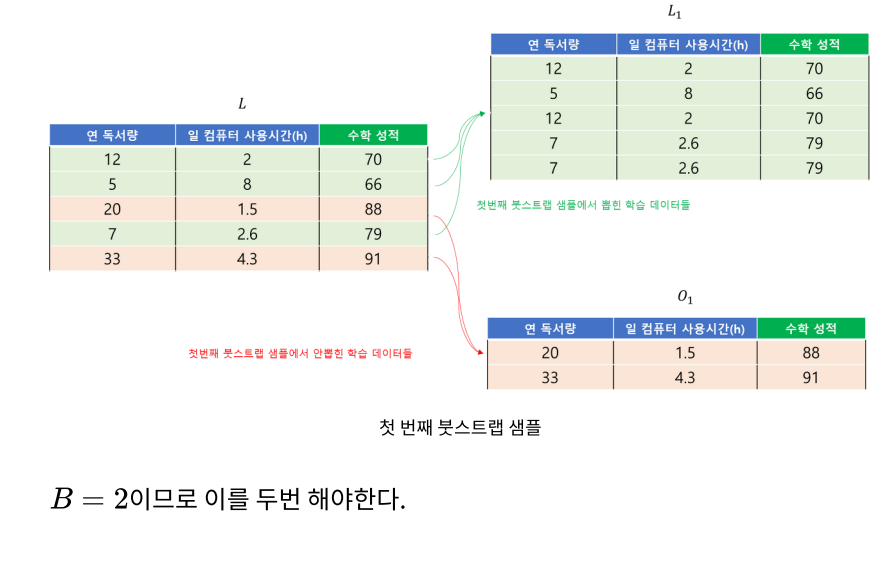



참고자료:https://zephyrus1111.tistory.com/245, Begging Predictors-Leo BREMIAN
'자격증 공부 > ADSP' 카테고리의 다른 글
| 로지스틱회귀분석 결과 해석 방법 (0) | 2023.05.01 |
|---|---|
| 신경망 모형 (0) | 2023.05.01 |
| 지역변수와 전역변수 (0) | 2023.05.01 |
| 의사결정나무 (0) | 2023.04.30 |
| 엔트로피의 이해 (0) | 2023.04.23 |