분산분석(anlaysis of variance:ANOVA)
1)개념
두 개 이상의 모집단에 대한 "모평균의 차이"를 비교할 때 사용하는 통계적 기법.
모집단이 두 개 일때라면 분산분석을 하지 않아도 상황에 따라 정규분포나 t분포를 이용하여 모평균의 차이를 분석할 수 있다.
만일 표본자료의 총 변동량 중에 급간변동이 차지하는 비중이 높다면 표본 간에 차이를 보게 된다는 것.
그러나 총변동량에서 급간변동이 차지하는 비중이 적다면 표본 자료의 변동은 급내변동에 의해 영향을 많이 받는다는 것이고 표본간에 유의한 차이를 발견할 수 없게 된다.
두 집단 간의 평균차이 : 독립표본 t검정
세 집단 이상의 평균차이: 일원배치 분산분석
일원배치 분산분석은 하나의 독립변수가 세 집단 이상으로 구성된 명목척도,종속변수는 숫자(연속형)로 된 등간 또는 비율척도여야 함
2)기본 가정
①종속변수는 등간척도 또는 비율척도여야 한다.
②모집단의 분포는 정규분포를 이루어야 한다.
③각 모집단의 분산(표준편차)는 동일해야 한다.
④각 집단의 표본은 독립적이어야 한다.
3)분산분석의 특징
①세 개 이상 집단 간의 모평균을 비교함이 목적이다.
②검정통계량은 F-분포를 사용한다.
③F값은 집단 간 분산을 집단 내 분산으로 나눈 값이다.
④모수적 가설검정법이다.
⑤집단 간 차이가 커지면 F값이 커진다.
⑥각 집단별 자료의 수가 다를 수 있다.
일원배치분산분석
일원배치 분산분석은 요인이 1개인 경우의 종속변수(반응변수)의 평균ㄴ차이 분석에 사용한다. 예를 들면, 교육수준에 따라 임금 창리르 분석하고자 할 때 사용한다.
(1)구조식

(2)가설 설정
일원배치 분산분석 가설
1.귀무가설(Ho):모든 집단의 평균은 같다. = 모든 집단의 평균에 차이가 없다.
['독립변수'와 '종속변수'의 관계가 '없을'것이다]라고 가정하는 것이 귀무가설
2.대립가설(H1):모든 집단의 평균이 모두 같지는 않다. = 적어도 두 집단간의 평균은 차이가 있다.
['독립변수'와 '종속변수'의 관계가 '있을'것이다]라고 가정하는 것이 대립가설
일원배치 분산분석의 조건
1.각 집단은 평균을 중심으로 정규분포: 각 집단의 n>30
2.각 집단의 분산은 모두 동일해야 함( 즉, 등분산)
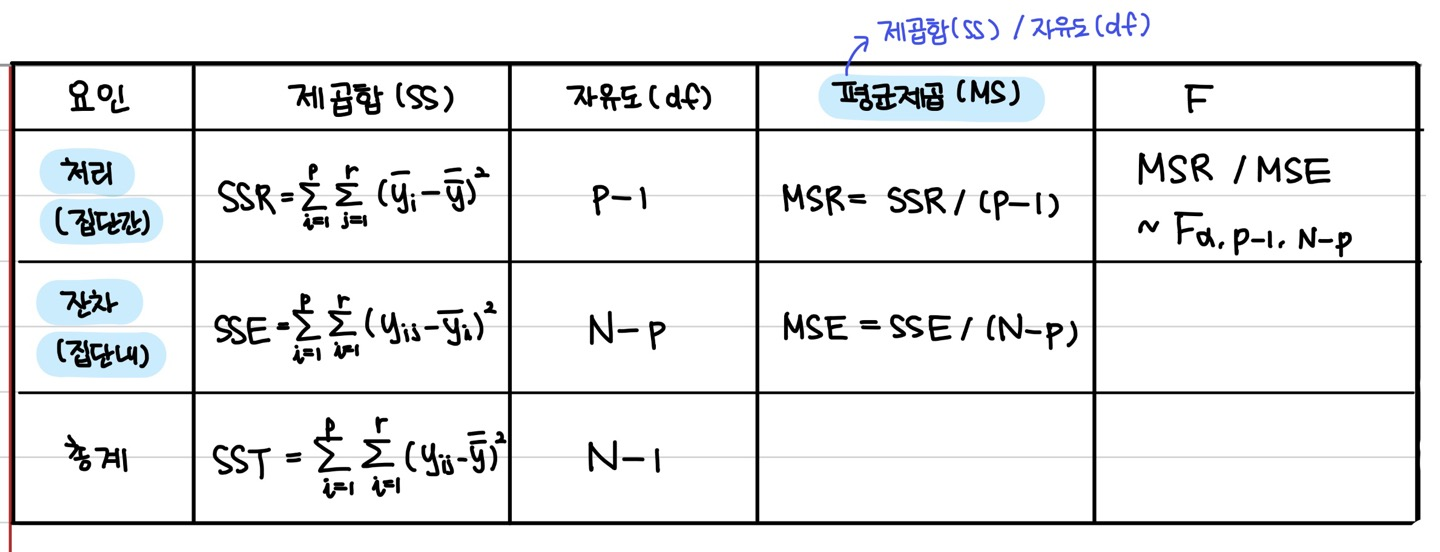
[일원배치분산분석표]
(1)변동의 분해
①P개의 요인수준을 각 r회 반복할 경우, 총 변동량을 요인간에 발생하는 변동과 잔차에 의해 발생하는 변동으로 분해

②위의 식에서 양변을 제곱하여 모든 i,j에 대하여 정리하면 다음과 같다.

ⓐ총제곱합(SST)
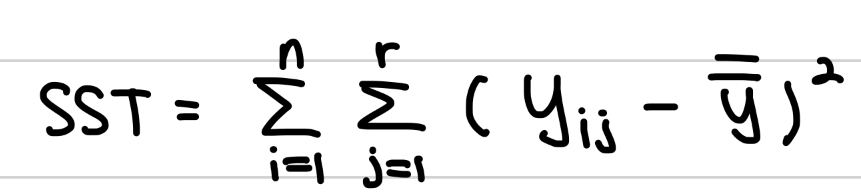
ⓑ처리(집단 간)제곱합(SSR)

ⓒ잔차(집단 내)제곱합(SSE)

[SPSS활용한 One-Way Anova]
1.등분산 조건 충족 여부
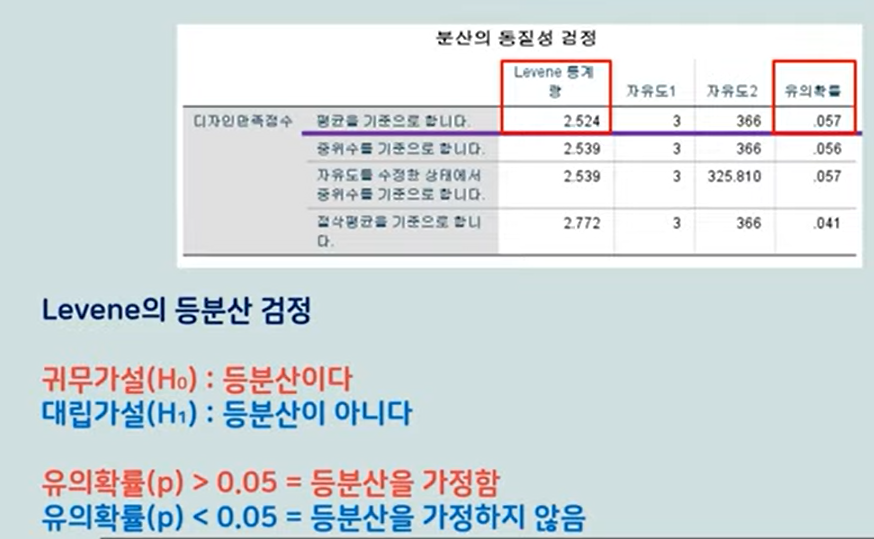
유의확률이 0.057이므로 등분산을 충족함
유의확률이 0.009이므로 귀무가설(H0) 기각, 대립가설(H1)채택
:직업 간 디자인 만족접수 평균은 모두 같진 않다. = 적어도 하나의 집단은 디자인 만족점수 평균 차이가 있다.
'직업'이라는 하나의 요인에 의해서 모평균이 같은지를 보는 것
https://www.youtube.com/watch?v=xNhXXb8A1v4
'개념 정리 > 통계(기초)' 카테고리의 다른 글
| 교차분석 (0) | 2022.05.12 |
|---|---|
| 이원분류분산분석 (0) | 2022.05.12 |
| 3.가설검정 문제 예시 (0) | 2022.05.12 |
| 3.가설검정 개념 (0) | 2022.05.11 |
| 2.신뢰구간의 추정 (0) | 2022.05.11 |